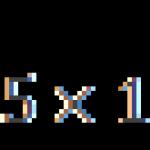Kako izračunati omjere. Kako napraviti proporciju? Svaki učenik i odrasla osoba će razumjeti omjer 1 0

Formula proporcija

Proporcija je jednakost dva omjera kada je a: b = c: d

odnos 1 : 10 je jednako omjeru 7 : 70, koji se takođe može napisati kao razlomak: 1 10 = 7 70 glasi: "jedan se odnosi na deset, kao i sedam na sedamdeset"

Osnovna svojstva proporcija

Umnožak ekstremnih članova jednak je proizvodu srednjih članova (unakrsno): ako je a: b = c: d, onda je a⋅d = b⋅c

1 10 ✕ 7 70 1 ⋅ 70 = 10 ⋅ 7

Inverzija proporcije: ako je a: b = c: d onda b: a = d: c

1 10 7 70 10 1 = 70 7

Permutacija srednjih članova: ako je a: b = c: d, onda je a: c = b: d

1 10 7 70 1 7 = 10 70

Permutacija ekstremnih članova: ako je a: b = c: d, onda je d: b = c: a

1 10 7 70 70 10 = 7 1

Rješavanje proporcija s jednom nepoznatom | Jednačina

1 : 10 = x : 70 ili 1 10 = x 70

Da biste pronašli x, trebate pomnožiti dva poznata broja unakrsno i podijeliti sa suprotnom vrijednošću

x = 1 ⋅ 70 10 = 7

Kako izračunati proporciju

Zadatak: potrebno je popiti 1 tabletu aktivnog ugljena na 10 kilograma težine. Koliko tableta treba uzeti ako osoba ima 70 kg?

Napravimo proporciju: 1 tableta - 10 kg x tablete - 70 kg Da biste pronašli x, trebate pomnožiti dva poznata broja unakrsno i podijeliti sa suprotnom vrijednošću: 1 tableta x pilule✕ 10 kg 70 Kg x = 1 ⋅ 70 : 10 = 7 odgovor: 7 tableta

Zadatak: Vasja napiše dva članka za pet sati. Koliko će članaka napisati za 20 sati?

Napravimo proporciju: 2 članka - 5 sati xčlanci - 20 sati x = 2 ⋅ 20 : 5 = 8 odgovor: 8 članaka

Mogu reći budućim maturantima da mi je dobro došla sposobnost pravljenja proporcija, i za proporcionalno smanjivanje slika, i u HTML izgledu web stranice, iu svakodnevnim situacijama.

Odnosom se naziva određeni odnos između entiteta našeg svijeta. To mogu biti brojevi, fizičke veličine, predmeti, proizvodi, pojave, radnje, pa čak i ljudi.

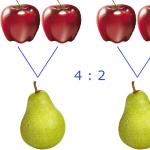
U svakodnevnom životu, kada su omjeri u pitanju, kažemo "Odnos ovoga i onoga"... Na primjer, ako se u vazi nalaze 4 jabuke i 2 kruške, onda kažemo "Odnos jabuke i kruške" "Odnos kruške i jabuke".

U matematici se omjer često koristi kao "Stav tog-i-toga prema tom-i-tom"... Na primjer, omjer četiri jabuke i dvije kruške, koji smo razmatrali gore, u matematici će glasiti kao "Omjer četiri jabuke prema dvije kruške" ili ako zamijenite jabuke i kruške, onda "Odnos dve kruške prema četiri jabuke".

Odnos se izražava kao a To b(gde umesto a i b bilo koje brojeve), ali češće možete pronaći unos koji je sastavljen pomoću dvotočka kao a: b... Ovaj unos možete pročitati na različite načine:

• a To b
• a odnosi se na b
• stav a To b

Zapišimo omjer četiri jabuke i dvije kruške koristeći simbol omjera:

4: 2

Ako zamijenimo mjesta jabuka i krušaka, onda ćemo imati omjer 2:4. Ovaj odnos se može čitati kao "dva do četiri" ili bilo koje "Dvije kruške se odnose na četiri jabuke" .

U nastavku ćemo taj omjer zvati omjerom.

Sadržaj lekcije

Šta je stav?

Relacija je, kao što je ranije spomenuto, zapisana u obliku a: b... Može se napisati i kao razlomak. A znamo da takva notacija u matematici znači podjelu. Tada će rezultat odnosa biti količnik a i b.

Omjer u matematici se naziva količnik dva broja.

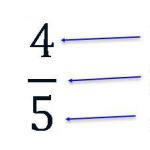
Omjer vam omogućava da saznate koliko jednog entiteta pada na jedinicu drugog. Vratimo se omjeru četiri jabuke prema dvije kruške (4:2). Ovaj omjer će nam omogućiti da saznamo koliko jabuka ima po jedinici kruške. Jedinica znači jedna kruška. Prvo, zapišimo omjer 4:2 kao razlomak:

Ovaj omjer je dijeljenje broja 4 sa brojem 2. Ako izvršimo ovo dijeljenje, dobićemo odgovor na pitanje koliko jabuka ima po jedinici kruške

Primljeno 2. Dakle, četiri jabuke i dvije kruške (4:2) koreliraju (međusobno su povezane) tako da postoje dvije jabuke po kruški

Slika pokazuje kako su četiri jabuke i dvije kruške povezane jedna s drugom. Vidi se da su za svaku krušku dvije jabuke.

Odnos se može obrnuti pisanjem kao. Tada dobijamo omjer dvije kruške prema četiri jabuke, odnosno "omjer dvije kruške prema četiri jabuke". Ovaj omjer će pokazati koliko krušaka ima po jedinici jabuke. Jedinica jabuka znači jedna jabuka.

Da biste pronašli vrijednost razlomka, morate zapamtiti kako podijeliti manji broj većim.

Primljeno 0,5. Pretvorimo ovaj decimalni razlomak u običan:

Smanjite rezultirajući razlomak za 5

Dobio odgovor (pola kruške). To znači da su dvije kruške i četiri jabuke (2:4) u korelaciji (međusobno povezane) tako da jedna jabuka čini polovicu kruške

Slika pokazuje kako su dvije kruške i četiri jabuke povezane jedna s drugom. Vidi se da na svaku jabuku dolazi polovina kruške.

Zovu se brojevi koji čine odnos članovi veze... Na primjer, u omjeru 4:2, članovi su brojevi 4 i 2.

Razmotrimo druge primjere odnosa. Da bi se nešto pripremilo, sastavlja se recept. Recept je izgrađen iz odnosa između proizvoda. Na primjer, za pravljenje ovsene kaše obično je potrebna čaša žitarica za dvije čaše mlijeka ili vode. Omjer je 1:2 ("jedan prema dva" ili "jedna čaša žitarica za dvije čaše mlijeka").

Omjer 1:2 pretvaramo u razlomak, dobijamo. Računajući ovaj razlomak, dobijamo 0,5. To znači da su jedna čaša žitarica i dvije čaše mlijeka međusobno povezane (međusobno povezane) tako da jedna čaša mlijeka čini pola čaše žitarica.

Ako obrnete odnos 1:2, dobijate omjer 2:1 („dva prema jedan” ili „dve čaše mleka za jednu čašu žitarica”). Pretvorimo omjer 2:1 u razlomak, dobijemo. Računajući ovaj razlomak, dobijamo 2. Dakle, dvije čaše mlijeka i jedna čaša žitarica su povezane (međusobno povezane) tako da na jednu čašu žitarica dolaze dvije čaše mlijeka.

Primjer 2. U razredu je 15 učenika. Od toga 5 dječaka, 10 djevojčica. Možete zapisati omjer djevojčica i dječaka 10:5 i pretvoriti taj omjer u razlomak. Računajući ovaj razlomak, dobijamo 2. To jest, djevojčice i dječaci su međusobno povezani na način da na svakog dječaka dolaze dvije djevojčice

Slika pokazuje kako se međusobno odnose deset djevojčica i pet dječaka. Vidi se da na svakog dječaka idu dvije djevojčice.

Omjer se ne može uvijek pretvoriti u razlomak i količnik se može naći. U nekim slučajevima to neće biti logično.

Dakle, ako preokrenete stav, ispada, a to je odnos dječaka prema djevojčicama. Ako izračunate ovaj razlomak, dobit ćete 0,5. Ispostavilo se da se pet dječaka odnosi na deset djevojčica na način da na svaku djevojčicu dolazi pola dječaka. Matematički je to naravno tačno, ali sa stanovišta stvarnosti nije sasvim razumno, jer je dječak živa osoba i ne možete ga tek tako uzeti i podijeliti, kao krušku ili jabuku.

Izgradnja ispravnog stava važna je vještina rješavanja problema. Dakle, u fizici, omjer prijeđene udaljenosti i vremena je brzina kretanja.

Udaljenost je označena promjenljivom S, vrijeme - kroz varijablu t, brzina - kroz varijablu v... Zatim fraza "Odnos pređene udaljenosti i vremena je brzina kretanja" biće opisan sledećim izrazom:

Pretpostavimo da je auto prešao 100 kilometara za 2 sata. Tada će omjer prijeđenih sto kilometara i dva sata biti brzina automobila:

Uobičajeno je da se brzina naziva udaljenost koju tijelo pređe u jedinici vremena. Jedinica vremena znači 1 sat, 1 minut ili 1 sekundu. A odnos, kao što je ranije spomenuto, omogućava vam da saznate koliko jednog entiteta pada na jedinicu drugog. U našem primjeru, odnos od sto kilometara do dva sata pokazuje koliko je kilometara potrebno za jedan sat kretanja. Vidimo da za svaki sat kretanja ide 50 kilometara.

Stoga se brzina mjeri u km/h, m/min, m/s... Simbol razlomka (/) označava omjer udaljenosti i vremena: kilometara na sat , metara u minuti i metara u sekundi respektivno.

Primjer 2... Odnos vrijednosti proizvoda i njegove količine je cijena jedne jedinice proizvoda

Ako smo uzeli 5 čokoladica iz trgovine i njihova ukupna cijena je bila 100 rubalja, tada možemo odrediti cijenu jedne pločice. Da biste to učinili, morate pronaći omjer od sto rubalja prema broju šipki. Onda dobijemo da postoji 20 rubalja za jednu šipku.

Poređenje količina

Ranije smo naučili da odnos između količina različite prirode formira novu količinu. Dakle, omjer prijeđenog puta i vremena je brzina kretanja. Odnos vrijednosti robe i njene količine je cijena jedne jedinice robe.

Ali omjer se također može koristiti za poređenje vrijednosti. Rezultat takvog odnosa je broj koji pokazuje koliko je puta prva vrijednost veća od druge ili koliki je dio prve vrijednosti od druge.

Da biste saznali koliko je puta prva vrijednost veća od druge, veća vrijednost mora biti upisana u brojiocu omjera, a manja vrijednost u nazivniku.

Da biste saznali koji je dio prve vrijednosti od druge, potrebno je da u brojiocu omjera upišete manju vrijednost, a u nazivnik veću vrijednost.

Razmotrimo brojeve 20 i 2. Hajde da saznamo koliko je puta broj 20 veći od broja 2. Da bismo to učinili, nalazimo omjer broja 20 i broja 2. U brojiocu omjera upisujemo broj 20, a u nazivniku - broj 2

Vrijednost ovog omjera je deset

Omjer broja 20 i broja 2 je broj 10. Ovaj broj pokazuje koliko je puta broj 20 veći od broja 2. Dakle, broj 20 je deset puta veći od broja 2.

Primjer 2. U razredu je 15 učenika. Od toga 5 dječaka, 10 djevojčica. Odredite koliko puta ima više djevojčica nego dječaka.

Zapisujemo odnos devojčica prema dečacima. Broj djevojaka upisujemo u brojilac veze, a broj dječaka u imenilac veze:

Vrijednost ovog omjera je 2. To znači da je u razredu od 15 djevojčica dvostruko više nego dječaka.

Više se ne postavlja pitanje koliko djevojčica ima za jednog dječaka. U ovom slučaju, omjer se koristi za poređenje broja djevojčica sa brojem dječaka.

Primjer 3... Koji je dio broja 2 od broja 20.

Pronalazimo odnos broja 2 i broja 20. U brojiocu odnosa upisujemo broj 2, a u nazivnik - broj 20

Da biste pronašli značenje ovog odnosa, morate se sjetiti

Vrijednost omjera broja 2 i broja 20 je broj 0,1

U ovom slučaju, decimalni razlomak 0,1 može se pretvoriti u običan. Ovaj odgovor će biti lakše razumjeti:

Dakle, broj 2 od broja 20 je jedna desetina.

Možete provjeriti. Da bismo to učinili, nalazimo od broja 20. Ako smo sve uradili ispravno, onda bismo trebali dobiti broj 2

20: 10 = 2

2 × 1 = 2

Dobili smo broj 2. Dakle, deseti dio broja 20 je broj 2. Stoga zaključujemo da je zadatak točno riješen.

Primjer 4. U razredu je 15 ljudi. Od toga 5 dječaka, 10 djevojčica. Odredite koliki udio od ukupnog broja školaraca čine dječaci.

Zapisujemo odnos dječaka prema ukupnom broju školaraca. U brojnik odnosa upisujemo pet dječaka, a u nazivnik ukupan broj učenika. Ukupan broj školaraca je 5 dječaka plus 10 djevojčica, pa u imenilac odnosa upisujemo 15

Da biste pronašli značenje ovog omjera, morate zapamtiti kako podijeliti manji broj većim. U ovom slučaju, broj 5 se mora podijeliti sa brojem 15

Kada podijelite 5 sa 15, dobijete periodični razlomak. Pretvorimo ovaj razlomak u običan

Dobili smo konačan odgovor. Dakle, dječaci čine jednu trećinu razreda.

Na slici se vidi da u odeljenju od 15 učenika 5 dečaka čini trećinu odeljenja.

Ako nađemo od 15 školaraca za provjeru, onda dobijemo 5 dječaka

15: 3 = 5

5 × 1 = 5

Primjer 5. Koliko je puta 35 veće od 5?

Zapisujemo omjer broja 35 i broja 5. U brojiocu omjera potrebno je upisati broj 35, u nazivnik - broj 5, ali ne i obrnuto

Vrijednost ovog omjera je 7. Dakle, broj 35 je sedam puta veći od broja 5.

Primjer 6. U razredu je 15 ljudi. Od toga 5 dječaka, 10 djevojčica. Odredite koliki je udio od ukupnog broja djevojčica.

Zapisujemo odnos djevojčica i ukupnog broja školaraca. U brojnik odnosa upisujemo deset djevojaka, a u nazivnik ukupan broj školaraca. Ukupan broj školaraca je 5 dječaka plus 10 djevojčica, pa u imenilac odnosa upisujemo 15

Da biste pronašli značenje ovog omjera, morate zapamtiti kako podijeliti manji broj većim. U ovom slučaju, broj 10 se mora podijeliti sa brojem 15

Kada podijelite 10 sa 15, dobijete periodični razlomak. Pretvorimo ovaj razlomak u običan

Dobijeni razlomak smanjite za 3

Dobili smo konačan odgovor. Dakle, djevojčice čine dvije trećine razreda.

Slika pokazuje da u odeljenju od 15 učenika dve trećine odeljenja čini 10 devojčica.

Ako nađemo od 15 školaraca za provjeru, onda dobijemo 10 djevojčica

15: 3 = 5

5 × 2 = 10

Primjer 7. Koji dio od 10 cm je 25 cm

Zapisujemo omjer deset centimetara prema dvadeset pet centimetara. U brojiocu omjera upisujemo 10 cm, u nazivnik 25 cm

Da biste pronašli značenje ovog omjera, morate zapamtiti kako podijeliti manji broj većim. U ovom slučaju, broj 10 se mora podijeliti sa brojem 25

Pretvorimo rezultujući decimalni razlomak u običan

Smanjite rezultirajući razlomak za 2

Dobili smo konačan odgovor. To znači da je 10 cm od 25 cm.

Primjer 8. Koliko puta je 25 cm više od 10 cm

Zapisujemo omjer dvadeset pet centimetara prema deset centimetara. U brojnik omjera upisujemo 25 cm, u nazivnik - 10 cm

Odgovor je bio 2,5. Znači 25 cm više od 10 cm 2,5 puta (dva i po puta)

Važna napomena. Prilikom pronalaženja omjera istoimenih fizičkih veličina, ove veličine moraju nužno biti izražene u jednoj mjernoj jedinici, inače će odgovor biti netačan.

Na primjer, ako imamo posla s dvije dužine i želimo da znamo koliko je puta prva dužina veća od druge, ili koji je dio prve dužine od druge, tada se obje dužine prvo moraju izraziti u jednoj jedinici mjerenje.

Primjer 9. Koliko puta je 150 cm više od 1 metra?

Prvo, napravimo tako da obje dužine budu izražene u istoj mjernoj jedinici. Da bismo to učinili, pretvorimo 1 metar u centimetre. Jedan metar je sto centimetara

1 m = 100 cm

Sada nalazimo omjer od sto pedeset centimetara prema sto centimetara. U brojiocu omjera pišemo 150 centimetara, u nazivniku - 100 centimetara

Nađimo vrijednost ovog omjera

Odgovor je bio 1,5. To znači da je 150 cm 1,5 puta više od 100 cm (jedan i po puta).

A ako nisu pretvorili metre u centimetre i odmah pokušali pronaći omjer od 150 cm prema jednom metru, onda bismo dobili sljedeće:

Ispostavilo bi se da je 150 cm više od jednog metra sto pedeset puta, ali to nije istina. Stoga je imperativ obratiti pažnju na jedinice mjerenja fizičkih veličina koje su uključene u odnos. Ako su ove količine izražene u različitim mjernim jedinicama, onda da biste pronašli omjer ovih veličina, morate prijeći na jednu mjernu jedinicu.

Primjer 10. Prošlog mjeseca plata je bila 25.000 rubalja, a ovog mjeseca plata je porasla na 27.000 rubalja. Odredite koliko je puta plata porasla

Zapisujemo odnos dvadeset sedam hiljada prema dvadeset pet hiljada. Zapisujemo 27000 u brojiocu omjera, 25000 u nazivniku.

Nađimo vrijednost ovog omjera

Odgovor je bio 1.08. To znači da je plata povećana za 1,08 puta. Ubuduće, kada budemo upoznali procente, takve pokazatelje kao što su plate iskazivaćemo u procentima.

Primjer 11... Širina stambene zgrade je 80 metara, a visina 16 metara. Koliko puta je kuća šira od svoje visine?

Zapisujemo omjer širine kuće i njene visine:

Vrijednost ovog omjera je 5. To znači da je širina kuće pet puta veća od njene visine.

Relationship property

Omjer se neće promijeniti ako se njegovi članovi pomnože ili podijele istim brojem.

Ovo je jedno od najvažnijih svojstava odnosa proizilazi iz svojstva posebnog. Znamo da ako se dividenda i djelitelj pomnože ili podijele istim brojem, tada se količnik neće promijeniti. A budući da odnos nije ništa drugo do podjela, svojstvo određenog također radi za njega.

Vratimo se na stavove djevojčica prema dječacima (10:5). Ovakav stav je pokazao da na svakog dječaka dolaze dvije djevojčice. Provjerimo kako funkcionira svojstvo relacije, naime, pokušajmo njegove članove pomnožiti ili podijeliti istim brojem.

U našem primjeru, zgodnije je podijeliti članove veze njihovim najvećim zajedničkim djeliteljem (GCD).

Gcd članova 10 i 5 je broj 5. Stoga se članovi veze mogu podijeliti brojem 5

Imam novi stav. Ovo je omjer dva prema jedan (2:1). Ovaj odnos, kao i prethodni omjer 10:5, pokazuje da su dvije djevojčice na jednog dječaka.

Na slici je prikazan odnos 2:1 (dva prema jedan). Kao i u prošlosti, odnos 10:5 po dječaku imaju dvije djevojčice. Drugim riječima, stav se nije promijenio.

Primjer 2... U jednom razredu ima 10 djevojčica i 5 dječaka. U drugom razredu ima 20 djevojčica i 10 dječaka. Koliko puta ima više djevojčica u prvom razredu nego dječaka? Koliko puta ima više djevojčica u drugom razredu nego dječaka?

U oba razreda je duplo više djevojčica nego dječaka, jer su veze i jednaki istom broju.

Svojstvo odnosa vam omogućava da izgradite različite modele koji imaju slične parametre kao i stvarni objekt. Pretpostavimo da je stambena zgrada široka 30 metara i visoka 10 metara.

Da biste nacrtali sličnu kuću na papiru, morate je nacrtati u istom omjeru 30:10.

Podijelite oba člana ovog omjera brojem 10. Tada ćemo dobiti omjer 3:1. Ovaj omjer je 3, baš kao i prethodni omjer 3

Pretvorimo metre u centimetre. 3 metra je 300 centimetara, a 1 metar je 100 centimetara

3 m = 300 cm

1 m = 100 cm

Imamo omjer 300 cm : 100 cm. Podijelite članove ovog omjera sa 100. Dobijamo omjer od 3 cm : 1 cm. Sada možemo nacrtati kuću širine 3 cm i visine 1 cm.

Naravno, nacrtana kuća je mnogo manja od prave kuće, ali omjer širine i visine ostaje nepromijenjen. To nam je omogućilo da nacrtamo kuću što je moguće bliže stvarnoj.

Stav se može shvatiti i na druge načine. Prvobitno je rečeno da prava kuća ima širinu od 30 metara i visinu od 10 metara. Ukupno je 30 + 10, odnosno 40 metara.

Ovih 40 metara može se shvatiti kao 40 dijelova. Omjer 30:10 znači da postoji 30 komada za širinu i 10 komada za visinu.

Dalje, članovi omjera 30:10 podijeljeni su sa 10. Rezultat je bio omjer 3:1. Ovaj odnos se može shvatiti kao 4 dijela, od kojih su tri za širinu, jedan za visinu. U ovom slučaju obično morate saznati koliko metara ima širina i visina.

Drugim riječima, trebate saznati koliko metara je u 3 dijela, a koliko metara je u 1 dijelu. Prvo morate saznati koliko metara ima jedan dio. Da biste to učinili, ukupno 40 metara mora biti podijeljeno sa 4, jer u omjeru 3: 1 postoje samo četiri dijela

Odredimo koliko metara ima širina:

10 m × 3 = 30 m

Odredimo koliko metara je na visini:

10 m × 1 = 10 m

Više članova veze

Ako je nekoliko članova dato u odnosu, onda se oni mogu shvatiti kao dijelovi nečega.

Primjer 1... Kupljeno 18 jabuka. Ove jabuke podijeljene su između mame, tate i kćeri u omjeru 2:1:3. Koliko je jabuka dobio svaki?

Omjer 2:1:3 znači da mama dobija 2 dijela, tata - 1 dio, kćerka - 3 dijela. Drugim riječima, svaki član omjera 2:1:3 je specifičan dio od 18 jabuka:

Ako zbrojite članove omjera 2:1:3, tada možete saznati koliko ukupno ima dijelova:

2 + 1 + 3 = 6 (dijelovi)

Saznajte koliko je jabuka u jednom dijelu. Da biste to učinili, podijelite 18 jabuka sa 6

18: 6 = 3 (jabuke po kriški)

Sada odredimo koliko je jabuka svaki dobio. Množenjem tri jabuke sa svakim članom omjera 2:1:3, možete odrediti koliko je jabuka dobila mama, koliko je dobio tata, a koliko ćerka.

Hajde da saznamo koliko je jabuka mama dobila:

3 × 2 = 6 (jabuke)

Saznajte koliko je tata dobio jabuka:

3 × 1 = 3 (jabuke)

Hajde da saznamo koliko je jabuka moja ćerka dobila:

3 × 3 = 9 (jabuke)

Primjer 2... Novo srebro (alpaka) je legura nikla, cinka i bakra u omjeru 3:4:13. Koliko kilograma svakog metala trebate uzeti da dobijete 4 kg novog srebra?

4 kilograma novog srebra sadržavat će 3 dijela nikla, 4 dijela cinka i 13 dijelova bakra. Prvo saznajemo koliko će dijelova biti u četiri kilograma srebra:

3 + 4 + 13 = 20 (dijelovi)

Odredimo koliko će kilograma biti u jednom dijelu:

4 kg: 20 = 0,2 kg

Odredimo koliko će kilograma nikla biti sadržano u 4 kg novog srebra. U omjeru od 3:4:13, tri dijela legure su naznačena da sadrže nikl. Dakle, množimo 0,2 sa 3:

0,2 kg × 3 = 0,6 kg nikla

Sada odredimo koliko će kilograma cinka biti sadržano u 4 kg novog srebra. U omjeru 3:4:13, za četiri dijela legure se kaže da sadrže cink. Dakle, množimo 0,2 sa 4:

0,2 kg × 4 = 0,8 kg cinka

Sada odredimo koliko će kilograma bakra biti sadržano u 4 kg novog srebra. U omjeru 3:4:13, za trinaest dijelova legure se kaže da sadrži bakar. Dakle, množimo 0,2 sa 13:

0,2 kg × 13 = 2,6 kg bakra

To znači da da biste dobili 4 kg novog srebra, potrebno je uzeti 0,6 kg nikla, 0,8 kg cinka i 2,6 kg bakra.

Primjer 3... Mesing je legura bakra i cinka, čija je težina 3: 2. Za izradu komada mesinga potrebno je 120 g bakra. Koliko je cinka potrebno da se napravi ovaj komad mesinga?

Odredimo koliko grama legure ima u jednom dijelu. Uslov kaže da je za izradu komada mesinga potrebno 120 g bakra. Takođe se kaže da tri dela legure sadrže bakar. Ako podijelimo 120 sa 3, saznaćemo koliko grama legure ima u jednom dijelu:

120: 3 = 40 grama po porciji

Sada odredimo koliko je cinka potrebno za izradu komada mesinga. Da biste to učinili, pomnožite 40 grama sa 2, jer je u omjeru 3: 2 naznačeno da dva dijela sadrže cink:

40 g × 2 = 80 grama cinka

Primjer 4... Uzeli smo dvije legure zlata i srebra. U jednom je količina ovih metala u omjeru 1:9, a u drugom 2:3. Koliko od svake legure treba uzeti da se dobije 15 kg nove legure, u kojoj bi se nalazilo zlato i srebro. odnos 1:4?

Rješenje

15 kg nove legure trebalo bi da bude u omjeru 1:4. Ovaj odnos sugerira da će jedan dio legure biti zlatni, a četiri dijela srebro. Ukupno ima pet dijelova. Ovo se može shematski prikazati na sljedeći način

Odredimo masu jednog dijela. Da biste to učinili, prvo dodajte sve dijelove (1 i 4), a zatim podijelite masu legure s brojem ovih dijelova

1 + 4 = 5
15 kg: 5 = 3 kg

Jedan dio legure će imati masu od 3 kg. Tada će 15 kg nove legure sadržavati 3 × 1 = 3 kg zlata i srebra 3 × 4 = 12 kg srebra.

Stoga, da bismo dobili leguru težine 15 kg, potrebno nam je 3 kg zlata i 12 kg srebra.

A sada da odgovorimo na pitanje problema - " Koliko od svake legure treba da uzmete? »

Uzet ćemo 10 kg prve legure, pošto su zlato i srebro u njoj u omjeru 1: 9. Odnosno, ova prva legura će nam dati 1 kg zlata i 9 kg srebra.

Uzet ćemo 5 kg druge legure, pošto su zlato i srebro u njoj u omjeru 2: 3. To jest, ova druga legura će nam dati 2 kg zlata i 3 kg srebra.

Da li vam se dopala lekcija?
Pridružite se našoj novoj Vkontakte grupi i počnite primati obavijesti o novim lekcijama

Osnova matematičko istraživanje je sposobnost da se stekne znanje o određenim veličinama upoređujući ih s drugim veličinama koje su ili su jednaki ili više ili manje nego one koje su predmet istraživanja. To se obično radi pomoću serije jednačine i proporcije... Kada koristimo jednadžbe, traženu vrijednost određujemo pronalaženjem jednakost sa nekom drugom već poznatom količinom ili količinama.

Međutim, često se dešava da nepoznatu količinu uporedimo sa drugim nije jednako nju, ali manje-više nju. To zahtijeva drugačiji pristup obradi podataka. Možda ćemo morati da saznamo, npr. koliko jedna količina je veća od druge, ili koliko puta jedno sadrži drugo. Da bismo pronašli odgovor na ova pitanja, naučit ćemo šta je odnos dve količine. Jedan omjer se zove aritmetika i drugi geometrijski... Vrijedi napomenuti, međutim, da oba ova termina nisu slučajno usvojena ili samo u svrhu razlikovanja. I aritmetički i geometrijski odnosi primjenjuju se i na aritmetiku i na geometriju.

Kao sastavnica jedne velike i važne teme, proporcija zavisi od proporcija, stoga je neophodno jasno i potpuno razumevanje ovih pojmova.

338. Aritmetički odnos to razlikaizmeđu dvije količine ili niza količina... Same količine se nazivaju članovi omjeri, odnosno pojmovi između kojih postoji odnos. Dakle, 2 je aritmetički omjer 5 i 3. To se izražava stavljanjem znaka minus između dvije vrijednosti, odnosno 5 - 3. Naravno, termin aritmetički omjer i njegovo škrabanje je praktično beskorisno, jer je samo riječ zamijenjen razlika znakom minus u izrazu.

339. Ako oba člana aritmetičke relacije umnožiti ili podijeliti za isti iznos onda omjer, na kraju će se pomnožiti ili podijeliti ovom vrijednošću.
Dakle, ako imamo a - b = r
Zatim pomnožimo obje strane sa h, (Ax. 3.) ha - hb = hr
I dijeljenjem sa h, (Ax. 4.) $ \ frac (a) (h) - \ frac (b) (h) = \ frac (r) (h) $

340. Ako se članovi aritmetičkog odnosa dodaju ili oduzmu od odgovarajućih članova drugog, onda će omjer zbira ili razlike biti jednak zbiru ili razlici dva omjera.
Ako je a - b
i d - h,
su dva odnosa,
Tada (a + d) - (b + h) = (a - b) + (d - h). Što je u svakom slučaju = a + d - b - h.
I (a - d) - (b - h) = (a - b) - (d - h). Što je u svakom slučaju = a - d - b + h.
Dakle, aritmetički omjer 11 - 4 je 7
A aritmetički omjer 5 - 2 je 3
Odnos zbira članova 16 - 6 je 10, zbir je omjera.
Omjer razlike pojmova 6 - 2 je 4, razlika je omjera.

341. Geometrijski odnos je odnos između količina, koji se izražava PRIVATNO ako se jedna količina podijeli s drugom.
Dakle, omjer 8 prema 4 može se zapisati kao 8/4 ili 2. To jest, količnik 8 prema 4. Drugim riječima, pokazuje koliko je puta 4 sadržano u 8.

Na isti način, omjer bilo koje količine prema drugoj može se odrediti dijeljenjem prve sa drugom ili, što je u principu isto, tako da prva bude brojnik razlomka, a druga nazivnik.
Dakle, omjer a prema b je $ \ frac (a) (b) $
Omjer d + h prema b + c je $ \ frac (d + h) (b + c) $.

342. Geometrijski odnos se takođe beleži postavljanjem dve tačke jedna iznad druge između vrednosti koje se porede.
Dakle, a: b je zapis omjera a prema b, a 12:4 je odnos 12 prema 4. Dvije veličine zajedno čine par u kojem se zove prvi pojam antecedent a posljednji je konsekventno.

343. Ovaj zapis uz pomoć tačaka i drugi, u obliku razlomka, zamjenjivi su po potrebi, dok antecedent postaje brojilac razlomka, a konsekvent postaje imenilac.
Dakle, 10:5 je isto što i $ \ frac (10) (5) $ i b: d, isto što i $ \ frac (b) (d) $.

344. Ako je od ove tri vrijednosti: antecedent, konsekvent i omjer, bilo koja dva onda se treći može naći.

Neka je a = antecedent, c = konsekvent, r = omjer.
Po definiciji, $ r = \ frac (a) (c) $, to jest, omjer je jednak antecedentu podijeljenom s posljedicom.
Množenjem sa c, a = cr, to jest, antecedent je jednak konsekventu pomnoženom omjerom.
Podijelite sa r, $ c = \ frac (a) (r) $, to jest, konsekvent je jednak antecedentu podijeljenom omjerom.

Dopisivanje 1. Ako dva para imaju jednake prethodnike i posljedice, onda su i njihovi omjeri jednaki.

Dopisivanje 2. Ako su za dva para omjeri i antecedenti jednaki, onda su posljedice jednake, a ako su omjeri i posljedice jednaki, onda su i antecedenti jednaki.

345. Ako se uporede dvije vrijednosti su jednaki, tada je njihov omjer jednak jedinici ili omjeru jednakosti. Omjer 3 * 6: 18 jednak je jedan, jer je količnik bilo koje količine podijeljene sa sobom jednak 1.

Ako je prethodnik para više, od posljedice, omjer je veći od jedan. Pošto je dividenda veća od djelitelja, količnik je veći od jedan. Dakle, omjer 18:6 je 3. To se zove omjer veća nejednakost.

S druge strane, ako je prethodnik manje od posljedice, tada je omjer manji od jedinice i to se zove omjer manje nejednakosti... Dakle, omjer 2:3 je manji od jedan, jer je dividenda manja od djelitelja.

346. Obrnuto omjer je omjer dvije recipročne vrijednosti.
Dakle, inverzni omjer od 6 prema 3 je k, to jest:.
Direktan omjer a prema b je $ \ frac (a) (b) $, to jest, antecedent se dijeli na konsekvent.
Inverzni odnos je $ \ frac (1) (a) $: $ \ frac (1) (b) $ ili $ \ frac (1) (a). \ Frac (b) (1) = \ frac (b) (a) $.
to jest, kosekvenca b podijeljena antecedentom a.

Dakle, izražena je inverzna relacija invertovanjem razlomka, koji prikazuje direktan odnos, ili, kada se snimanje vrši pomoću tačaka, obrnuti redosled članova.
Dakle, a se odnosi na b na isti način kao b na a.

347. Kompleksni odnos ovaj odnos radi odgovarajući pojmovi sa dva ili više jednostavnih odnosa.
Dakle, odnos 6:3 je 2
I omjer 12:4 je jednako 3
Odnos koji se sastoji od njih je 72:12 = 6.

Ovdje se složeni odnos dobija množenjem dva antecedenta između sebe i dvije posljedice jednostavnih odnosa.
Dakle, omjer je napravljen
Iz omjera a: b
I omjer c: d
i odnos h: y
Ovaj omjer je $ ach: bdy = \ frac (ach) (bdy) $.
Omjer spoja se ne razlikuje po svom priroda iz bilo kojeg drugog omjera. Ovaj izraz se koristi da pokaže porijeklo veze u određenim slučajevima.

Dopisivanje Kompleksni omjer jednak je proizvodu jednostavnih omjera.
Omjer a: b je jednak $ \ frac (a) (b) $
Omjer c: d je jednak $ \ frac (c) (d) $
Omjer h:y je $ \ frac (h) (y) $
A omjer koji se dodaje od ova tri bit će ach/bdy, što je proizvod razlomaka koji izražavaju jednostavne omjere.

348. Ako je u nizu omjera u svakom prethodnom paru konsekvent prethodnik u sljedećem, tada omjer prvog antecedenta i posljednjeg posljedičnog jednak je onom dobivenom iz međuodnosa.
Dakle, u brojnim odnosima
a: b
b: c
c: d
d: h
omjer a: h jednak je omjeru dodanom iz omjera a: b i b: c i c: d i d: h. Dakle, kompleksni omjer u posljednjem članku je $ \ frac (abcd) (bcdh) = \ frac (a) (h) $, ili a: h.

Na isti način, sve količine koje su i antecedentne i posljedične nestati, kada će proizvod razlomaka biti pojednostavljen na svoje najniže članove, a u ostatku će kompleksni omjer biti izražen prvim antecedentom i posljednjom posljedicom.

349. Posebna klasa složenih relacija dobija se množenjem jednostavne relacije sa sebe ili nešto drugo jednaka odnos. Ovi omjeri se nazivaju duplo, trostruko, quads, i tako dalje, prema broju operacija množenja.

Odnos sastavljen od dva jednaki omjeri, tj. kvadrat duplo odnos.

Sastavljeno od tri, to je, kocka prosta relacija se nazivaju trostruko, itd.

Slično, omjer kvadratni korijeni dvije veličine nazivamo omjerom kvadratni korijen i omjer kubnih korijena- odnos kubni korijen, itd.
Dakle, jednostavan omjer a prema b je a: b
Dvostruki omjer a prema b jednak je a 2: b 2
Trostruki omjer a prema b jednak je a 3: b 3
Omjer kvadratnog korijena a prema b je √a: √b
Omjer kubnog korijena a prema b je 3 √a: 3 √b, i tako dalje.
Uslovi duplo, trostruko, i tako dalje ne treba miješati sa udvostručeno, utrostručio, itd.
Odnos 6 prema 2 je 6:2 = 3
Udvostručavajući ovaj omjer, odnosno omjer dvaput, dobijamo 12:2 = 6
Utrostručimo ovaj omjer, odnosno ovaj omjer tri puta, onda dobijemo 18: 2 = 9
A duplo odnos, tj kvadrat omjer je 6 2 : 2 2 = 9
I trostruko omjer, odnosno kocka omjera je 6 3: 2 3 = 27

350. Da bi veličine bile u međusobnoj korelaciji, moraju biti iste vrste, tako da se može pouzdano tvrditi da li su jedna drugoj jednake, ili je jedna od njih veća ili manja. Stopa je kao 12 prema 1 u odnosu na inč: 12 puta je veća od inča. Ali ne može se reći, na primjer, da je sat duži ili kraći od štapa, ili da je ar veći ili manji od stepena. Međutim, ako su te količine izražene u brojevi, onda može postojati odnos između ovih brojeva. Odnosno, može postojati odnos između broja minuta po satu i broja koraka po milji.

351. Okrećući se na priroda omjera, u sljedećem koraku trebamo uzeti u obzir način na koji će promjena u jednom ili dva člana, koji se međusobno upoređuju, uticati na sam omjer. Podsjetimo da se direktni omjer izražava kao razlomak, gdje antecedet parovi uvek to brojilac, a konsekventno - imenilac... Tada će iz svojstva razlomaka biti lako dobiti da se promjene u omjeru dešavaju variranjem upoređenih vrijednosti. Omjer dvije veličine je isti kao značenje razlomci, od kojih svaki predstavlja privatni: brojilac podijeljen nazivnikom. (Član 341.) Sada se pokazalo da je množenje brojioca razlomka bilo kojom vrijednošću isto što i množenje značenje sa istim iznosom i dijeljenje brojila je isto kao i dijeljenje vrijednosti razlomka. dakle,

352. Množenje prethodnika para bilo kojom vrijednošću znači množenje omjera ovom vrijednošću, a dijeljenje prethodnika je dijeljenje ovog omjera.
Dakle, odnos 6:2 je 3
A omjer 24:2 je jednak 12.
Ovdje je antecedent i omjer u posljednjem paru 4 puta veći nego u prvom.
Omjer a: b je $ \ frac (a) (b) $
A omjer na: b je jednak $ \ frac (na) (b) $.

Dopisivanje Uz poznatu posljedicu, to više antecedent, više odnos, i obrnuto, što je veći omjer, veći je prethodnik.

353. Množenjem konsekventa para bilo kojom vrijednošću, kao rezultat, dobijamo podjelu omjera sa ovom vrijednošću, a dijeljenjem konsekventa množimo omjer. Množenjem nazivnika razlomka dijelimo vrijednost, a dijeljenjem nazivnika vrijednost se množi.
Dakle, odnos 12:2 je 6
A odnos 12:4 je 3.
Evo posljedice drugog para u dvaput više i odnos dvaput manje od prvog.
Omjer a: b je $ \ frac (a) (b) $
A omjer a: nb je jednak $ \ frac (a) (nb) $.

Dopisivanje Sa datim antecedentom, što je posljedica veća, to je omjer niži. Suprotno tome, što je veći omjer, to je posljedica manja.

354. Iz posljednja dva člana proizilazi da množenje antecedenta par za bilo koji iznos će imati isti učinak na omjer kao podjela posljedice za ovaj iznos, i podjela antecedenta, imaće isti efekat kao posljedično množenje.
Dakle, omjer 8:4 je jednak 2
Množenjem antecedenta sa 2, odnos 16:4 je 4
Deljenjem antecedenta sa 2, odnos 8:2 je 4.

Dopisivanje Bilo koji faktor ili razdjelnik može se prenijeti sa antecedenta para u konsekvent ili iz konsekventa u antecedent bez promjene omjera.

Vrijedi napomenuti da kada se faktor tako prenese iz jednog člana u drugi, on postaje djelitelj, a preneseni djelitelj postaje faktor.
Dakle, odnos je 3,6:9 = 2
Prenošenje faktora 3, $ 6: \ frac (9) (3) = 2 $
isti odnos.

Odnos $ \ frac (ma) (y): b = \ frac (ma) (by) $
Prenošenje y $ ma: by = \ frac (ma) (by) $
Kretanje m, a: $ a: \ frac (m) (by) = \ frac (ma) (by) $.

355. Kao što je očigledno iz čl. 352 i 353, ako se prethodni i konsekventni pomnože ili podijele sa istom vrijednošću, tada se omjer ne mijenja.

Dopisivanje 1. Odnos dva razlomci, koji imaju zajednički imenitelj, jednak je omjeru njihovih brojioci.
Dakle, omjer a / n: b / n je isti kao a: b.

Dopisivanje 2. Direktno omjer dva razlomka koji imaju zajednički brojnik jednak je inverznom omjeru njihovog imenioci.

356. Iz članka je lako odrediti omjer bilo koja dva razlomka. Ako se svaki član pomnoži sa dva nazivnika, onda će omjer biti dat integralnim izrazima. Dakle, množenjem članova para a / b: c / d sa bd, dobijamo $ \ frac (abd) (b) $: $ \ frac (bcd) (d) $, koji postaje ad: bc, smanjenjem zajedničke vrijednosti iz brojnika i nazivnika.

356. b. Ratio veća nejednakost povećava njegov
Neka je omjer veće nejednakosti 1 + n: 1
I bilo koji omjer kao a: b
Složeni odnos bi bio (čl. 347,) a + na: b
Što je veće od odnosa a: b (čl. 351. odn.)
Ali omjer manje nejednakosti presavijeno u drugom omjeru, smanjuje njegov.
Neka je omjer manje razlike 1-n: 1
Bilo koji dati omjer a: b
Kompleksni odnos a - na: b
Što je manje od a: b.

357. Ako do ili od članova bilo kojeg paradodati ili oduzmite dvije druge količine koje su u istom omjeru, tada će zbroji ili bilansi imati isti omjer.
Neka je omjer a: b
Biće isto kao c: d
Zatim odnos sume prethodnici zbiru posledica, naime, a + c do b + d, takođe su isti.
To jest, $ \ frac (a + c) (b + d) $ = $ \ frac (c) (d) $ = $ \ frac (a) (b) $.

Dokaz.

1.Prema pretpostavci, $ \ frac (a) (b) $ = $ \ frac (c) (d) $
2. Pomnožite sa b i d, ad = bc
3. Dodajte cd na obje strane, ad + cd = bc + cd
4. Podijelite sa d, $ a + c = \ frac (bc + cd) (d) $
5. Podijelite sa b + d, $ \ frac (a + c) (b + d) $ = $ \ frac (c) (d) $ = $ \ frac (a) (b) $.

Ratio razlike prethodnice posljedične razlike su također iste.

358. Ako su u nekoliko parova omjeri jednaki, onda zbir svih antecedenta odnosi se na zbir svih posljedičnih, kao i svaki prethodnik njegovoj konsekventnoj.
Dakle, omjer
|12:6 = 2
|10:5 = 2
|8:4 = 2
|6:3 = 2
Dakle, omjer (12 + 10 + 8 + 6) :( 6 + 5 + 4 + 3) = 2.

358. b. Ratio veća nejednakostsmanjuje se dodavanje istu vrijednost za oba člana.
Neka je data relacija a + b: a ili $ \ frac (a + b) (a) $
Dodavanjem x oba člana, dobijamo a + b + x: a + x ili $ \ frac (a + b) (a) $.

Prvi postaje $ \ frac (a ^ 2 + ab + ax + bx) (a (a + x)) $
I posljednji je $ \ frac (a ^ 2 + ab + ax) (a (a + x)) $.
Pošto je posljednji brojilac očito manji od drugog, onda odnos trebalo bi da bude manje. (čl. 351. odn.)

Ali omjer manje nejednakosti povećava dodavanjem istog iznosa oba termina.
Neka je data relacija (a-b): a, ili $ \ frac (a-b) (a) $.
Dodavanjem x na oba pojma dobija se oblik (a-b + x) :( a + x) ili $ \ frac (a-b + x) (a + x) $
Dovodeći ih do zajedničkog nazivnika,
Prvi postaje $ \ frac (a ^ 2-ab + ax-bx) (a (a + x)) $
I posljednji, $ \ frac (a ^ 2-ab + ax) (a (a + x)). \ Frac ((a ^ 2-ab + ax)) (a (a + x)) $.

Pošto je zadnji brojilac veći od drugog, onda odnos više.
Ako umjesto dodavanja iste vrijednosti oduzmi iz dva člana, očigledno je da će efekat na odnos biti suprotan.

Primjeri.

1. Što je veće: odnos 11:9 ili omjer 44:35?

2. Što je veće: omjer $ (a + 3): \ frac (a) (6) $, ili omjer $ (2a + 7): \ frac (a) (3) $?

3. Ako je prethodnik para 65, a omjer 13, koja je posljedica?

4. Ako je konsekvent para 7, a omjer 18, koji je antecedent?

5. Kako izgleda kompleksni odnos sastavljen od 8:7, i 2a:5b, kao i (7x + 1) :( 3y-2)?

6. Kako izgleda kompleksni omjer sastavljen od (x + y): b, i (x-y) :( a + b), kao i (a + b): h? Resp. (x 2 - y 2): bh.

7. Ako omjeri (5x + 7) :( 2x-3) i $ (x + 2): \ lijevo (\ frac (x) (2) +3 \ desno) $ formiraju kompleksan omjer, onda koji omjer će se dobiti: više ili manje nejednakosti? Resp. Odnos veće nejednakosti.

8. Koji je omjer sastavljen od (x + y): a i (x - y): b, i $ b: \ frac (x ^ 2-y ^ 2) (a) $? Resp. Odnos jednakosti.

9. Koliki je omjer 7:5 i dvostruko veći omjer 4:9 i trostruki omjer 3:2?
Resp. 14:15.

10. Koji je omjer sastavljen od 3:7 i trostrukog x:y omjera i ekstrakcije korijena iz omjera 49:9?
Resp. x 3: y 3.